CONTOS

1. A GAROTA DE ROSTO AVERMELHADO
2. O SENTIDO DA VIDA
3. SÓ, NUMA NOITE, NUMA ESTRADA
4. A BORBOLETA DO MAL

7x13=28?

Não compreender bem a estrutura de formação dos números na representação decimal pode acarretar a erros de cálculo que normalmente passam desapercebido para quem está resolvendo um exercício.

Todo sabemos (ou espero que saibamos) que o resultado de 7x13 é 91 e não 28. No vídeo abaixo a dupla de humorista dos anos 40, Abbott e Costello, mostram uma manipulação na conta 7x13 onde o resultado é 28.

O vídeo mostra o que acontece quando desrespeitamos a ordem das dezenas e das unidades dos números.

MATEMÁTICA

I. ENSINO MÉDIO

1. FUNÇÕES

. . 1.1. Função Do 2º Grau
. . 1.1.1 Vertice da função do 2º grau

2. SEQUÊNCIAS E PROGRESSÕES

. . 2.1. Sequências Numéricas

. . 2.2. Progressão Aritmética
. . 2.3. Interpolação Aritmética
. . 2.4. Soma da PA

3. SIMULADO

II. ENSINO SUPERIOR

1. ÁLGEBRA

. . 1.1. Aritmética Modular

. . 1.2. Grupos

. . 1.2.1. Introdução, definição e conceito

RPG

1. JOGO DE INTERPRETAÇÃO DE PAPÉIS
2. NASCE UM PERSONAGEM
3. ENTRANDO EM CENA

Grupos - Introdução

1. INTRODUÇÃO

O conceito de grupo é uma forma generalizada de trabalhar com diversos elementos da matemática que têm algo em comum, porem que seria exaustivo deduzir separadamente suas propriedades. Por exemplo, tome o conjunto dos números inteiros Z e o conjunto das matrizes de números reais 2x2. Em cada um destes conjunto temos definidas duas operações chamadas soma e multiplicação, embora a soma se inteiros seja diferente da soma de matrizes há certas semelhanças entre elas, como a existência de um elemento que somado com qualquer outro do conjunto dá como resultado este qualquer outro, somar a+b é o mesmo que somar b+a seja a e b números ou matrizes, para cada elemento (número ou matriz) existe um outro que somado a este dá o elemento neutro. A representação do que foi falado acima pode ser visto no esquema abaixo:




Podemos fazer algumas comparações entre estes dois conjunto também relativo a multiplicação, a diferença aqui é que o produto de duas matrizes pode dar zero e nem sempre AB=BA quando A e B são matrizes.

O objeto grupo foi inicialmente associado a resoluções de equações polinomiais de grau maior que 4. Até a época de 1824 vários matemáticos se empenhavam em encontrar uma formula para resolução de equações polinomiais de grau maior ou igual a cinco. Entretanto Niels Abel deu uma demonstração de que não há uma formula geral de resolução para equações de grau 5 ou acima evolvendo apenas as operações básicas e a estração de raiz.

Evariste Galois alguns anos depois estabeleceu um critério que diz quando um equação pode ser resolvida a partir das operações mencionadas acima. Galois havia associado as raízes da equação a um conjunto onde era definida uma operação, a partir das propriedades deste conjunto poderia dizer se era possível ou não resolver a equação a partir de radicais. Galois chamou este conjunto com a respectiva operação de Grupo.


2. DEFINIÇÃO E CONCEITO

Dado um conjunto G, uma operação neste conjunto é uma aplicação *:GXG→G onde *(a,b)=a*b. Em outras palavras, uma operação em um conjunto G é uma regra que associa capa par de elementos a e b a um outro elemento a*b em G.
Dado um conjunto G onde está definida uma operação *, chamamos a estrutura (G,*) de grupo se a operação * satisfaz as seguintes condições:

Note que aqui não estamos assumindo necessariamente que a operação seja comutativa, isto é, a*b=b*a. Caso isto aconteça o grupo é chamado grupo comutativo, ou grupo abeliano em homenagem ao matemático Niels Abel.

Note que a partir desta definição podemos fazer algumas inferências das propriedades de operações e conjuntos diversos. No exemplo anterior tanto o conjunto dos inteiros com das matrizes com suas respectivas somas satisfazer as condições de grupos, logo são grupos. Os números racionais, exeto o zero, com a multiplicação também satisfaz as condições de grupos.

Além dos exemplos citados acima podemos encontrar exemplos mais sutís de grupos, como as simetrias de um triângulo equilátero (conhecido como grupos Diametral 3), as permutações de objetos, diferentes subconjunto numéricos, entre outros

Por um fio

Imagine um fio extenso o bastante, capaz de dar a volta no planeta Terra. Imagine que a Terra seja uma esféra perfeita e que este fio é mondado em uma cincunferência encima da superfície da Terra (Figura 1). Agora imagine que a esse fio é acrescentado mais um metro de fio, e o novo comprimento é moldado em uma circunferência perfeita com o mesmo raio que a anterior. Desta nova circunferência existe uma folga entre a superfície da Terra e o fio (Figura 2). Pergunta: Um gato consegue passar por esta folga?


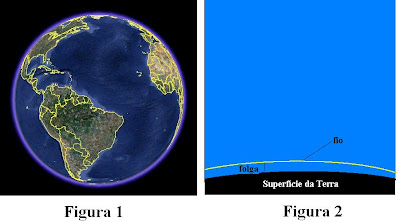
A primeira vista diriamos sem exitar que é impossível um gato passar por esta folga, pois só foi aumentado um metro a mais no fio e isso não produz uma variação significativa no raio da circunferência do fio. Para saber então qual é esta folga vamos calcular esta diferença.

O raio da Terra é aproximadamente 6 355 000 m. A relação que descreve o comprimento de uma circunferência C em função do seu raio r é onde é aproximadamente 3,14159.

Assim, a circunferência da terra é 2 . 6 355 000 . = 39 929 608, 9 m. A este comprimento foi aumentado 1 metro de fio ficando com 39 929 609, 9 m. A relação inversa, que descreve o raio em função do comprimento da circunferência, é . Usando esta relação para encontrar o raio da circunferência do fio temos r= 39 929 609, 9/(2x3,14159)= 6 355 000, 159 m.

A folga entre a superfície da Terra e do fio é portanto 6 355 000-6 355 000, 159=0,159 m, aproximadamente 16 cm.

Não é difícil imaginar um gato, mesmo que arrastado, passando por baixo de uma fresta de 16 cm.

Enquanto isso

Pavê

Ontem mesmo eu fiz um pavê e queria compartilhar com todos aqueles que lêem este blog.



Olhem, podem ver.