Adriano GS: 2010

sexta-feira, 24 de dezembro de 2010

Eu, tu e ele (Onde está o erro?)

Então me diga, ONDE ESTA O R$ 1,00 ?!

Resolva o Problema:

Eu, Tu e Ele... fomos comer no restaurante e no final a conta deu R$30,00.

Fizemos o seguinte: cada um deu dez reais...
Eu: R$ 10,00
Tu: R$ 10,00
Ele: R$ 10,00

O garçom levou o dinheiro até o caixa
e o dono do restaurante disse o seguinte:

- Esses três são clientes antigos do restaurante,
então vou devolver R$5,00 para eles!
E entregou ao garçom cinco moedas de R$ 1,00.

O garçom, muito esperto, fez o seguinte: pegou R$ 2,00 para ele
e deu R$1,00 para cada um de nós.

No final ficou assim:
Eu: R$ 10,00 (-R$1,00 que foi devolvido) = Eu gastei R$9,00.
Tu: R$ 10,00 (-R$1,00 que foi devolvido) = Tu gastaste R$9,00.
Ele:R$ 10,00 (-R$1,00 que foi devolvido) = Ele gastou R$9,00.

Logo, se cada um de nós gastou R$ 9,00
somando, juntos gastamos R$ 27,00

E se o garçom pegou R$2,00 para ele, temos:
Nós: R$27,00
Garçom: R$2,00
TOTAL: R$29,00

quarta-feira, 15 de dezembro de 2010

Faz sentido

1

Pai: Filho, Vá e regue a horta.
Filho: Mas pai, está chovendo!
Pai: Deixa de preguiça, pega o guarda-chuva e anda logo!!!

2

Mão: Por que será que os cachorros estão latindo lá fora?
Filho: Porque são cachorros, se fossem gatos miavam.

3

Amigo1: Posso lhe fazer uma pergunta?
Amigo 2: Mas não acabou de fazer?
Amigo 1: Certo, certo. Posso lhe fazer outra pergunta?
Amigo2: Você realmente não me dá escolha.

4

Filho: Pai, qual o nome desta fruta?
Pai: É ameixa preta.
Filho: Mas por que ela está vermelha?
Pai: Porque ainda está verde.

sexta-feira, 10 de dezembro de 2010

Tangram

Pegue uma folha no formato de um quadrado. Para facilitar, nomeie os vértices do quadrado como A, B, C e D como na figura 1;

Divida o quadrado ao meio traçando a diagonal AC;

Encontre M, o ponto médio de AD e N, o ponto médio de CD e trace o segmento MN;

Encontre O, o ponto médio de MN e trace o segmento BO;

Chame de E o ponto médio de AC;

Encontre F, o ponto médio de CE e trace o segmento FO;

Encontre G, o ponto médio de AE e trace o segmento GM.

O resultado final disso é o tangram como na figura abaixo. Pinte e recorte as partes encima dos segmentos traçados.

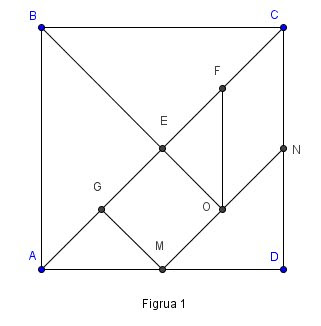Se sua pergunta for: O que eu vou fazer com isso? Bom, uma das alternativas é começar a tentar montar uma das figuras abaixo:

sábado, 20 de novembro de 2010

Quebra-cabeça

terça-feira, 14 de setembro de 2010

Visualização de gráficos com Winplot

segunda-feira, 23 de agosto de 2010

O problema do milênio "P versus NP" pode ter sido resolvido.

O pesquisador Vinay Deolalikar, que trabalha em Hewlett-Packard em Palo Alto, Califórnia, acredita ter resolvidos um dos problemas do milênio estabelecido no ano de 2000 pelo Clay Mathematical Institute.

No ano de 2000 a Clay Mathematical Institutede Cambridge, Massachusetts (CMI), para celebrar a matemática do terceiro milênio, estabeleceu o Millennium Prize Problems, um prémio de 7 milhão de dólares para a solução de sete problemas estabelecidos pela instituição, 1 milhão para cada problema.

Os problemas escolhidos pelo Instituto são questões matemáticas que permaneceram, e alguns ainda permanecem, sem solução por séculos, mas que as soluções se encontradas seria uma grande contribuição para a ciência da Matemática e outras como a Física e a Computação.

A resolução do problemas de Vinay Deolalikar, que ainda está em banca para avaliação, está relacionado com problemas computacionais de algoritmos. A Ciência da Computação classifica o tempo de execução dos algoritmo de duas formas: P, que significa polinomial, são os algoritmos cujo tempo de execução são rápidos e viáveis para serem implementados pois este tempo se compara ao crescimento de uma função polinomial da entrada; e E, que significa exponencial, são os algoritmos cujo tempo de execução se compara a uma função exponencial da entrada. Estes últimos algoritmos são lentos e na maioria das vezes inviáveis de serem implementados.

Ah entretanto uma outra classe denominada NP (não-polinomiais), esta classe seria um meio termo entre os algoritmos P e E. Acretitava-se que o conjunto dos problemas NP seria na verdade uma classe mascarada dos problemas P. A proposata de demonstação de Vinay Deolalikar vem dizer o contrário, que NP é diferente de P.

QUAIS SÃO OS OUTROS PROBLEMAS:

Os ostros problemas selecionados pelo Clay Mathematical Institutede são:

1. A Hipótese de Rieman

Este problema tenta estabelecer, se existe, a ordem com a qual os número primos estão distribuídos dentro do conjunto dos números naturais. Por exemplo, da sequência dos números primos 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ... parece não existir um padrão que diga qual é o próximo número, ou uma formula que de o n-ésimo número primo.

2. Teoria de Yang-Mills e a Hipótese da Lacuna da Massa

Esta questão tenta caracterizar forças forças da natureza diferentes da gravidade que, apesar de observadas em laboratório, não foram verificadas matematicamente. Este problema tenta trabalhar estas questões no espaço quadridimencional euclidiano.

3. P versus NP

Como dito acima. Este problema tenta estabelecer se a classo dos problemas NP é subconjunto da classe dos problemas P. Problema este provávemente resolvido por Vinay Deolalikar em 2010.

4. As equações de Navier - Stokes

Este problema tenta descrever, a partir das equações estabelecidas por Claude-Louis Navier e George Gabriel Stokes, o comportamento de fluidos em movimento como a água em torno de um barco, ou o ar em torno de uma aeronave.

5. A conjectura de Poincaré

"Se uma variedade de 3 dimensões é conexa e simplesmente conexa, então ela é uma esfera de 3d". Esta conjectura tenta classificar as variedades de dimensão 3. Por exemplo, a superfície de uma esfera á a variedade conexa mais simples de 2 dimensões. Nesta conjectura Poincaré acreditava que a superfície da esfera de 4 dimensões (a superficie tem 3 dimensões) seria a variedade conexa mais simples de 3 dimensões. A conjectura de Poincaré foi provada em 2002 pelo matemático Grigori Perelman que recusou o prémio e a medalha Fields, prémio equivalente ao Nobel da Matemática.

6. A conjectura de Birch e Swinnerton-Dyer

Esta conjectura é parecida com o "Último Teorema de Fermat" demonstrado em 1993 por Andrew Wiles. Wiles demonstrou que a equação [; x^n+y^n=z^n ;]

não possui solução para [; n ;]

maior ou igual a 3. Para equações mais complexas fica difícil saber se existe soluções e como elas são. A conjectura de Birch e Swinnerton-Dyer fornece possíveis soluções para alguns casos.

7. A conjectura de Hodge

Esta conjectura propõem que objetos matemáticos complicados podem ser construídos a partir de outros objetos mais simples. Uma forma rústica de pensar nisto é imaginar que um bastão de baseball pode ser construídos a partir de esferas e cilindros. Hodge sugeriu que as equações capazes de descrever determinados formatos cíclicos em várias dimensões poderiam ser geradas a partir de formas geométricas mais simples, similares a curvas.

Para saber mais sobre o Millennium Prize Problems visite os links:

http://www.hpl.hp.com/personal/Vinay_Deolalikar/
http://www.dm.ufscar.br/hp/hp501/hp501001/hp501001.html
http://www.livrariadafisica.com.br/detalhe_produto.aspx?id=24593
http://www.claymath.org/millennium/
http://mp-matematicaaplicada.blogspot.com/2008/10/os-seis-problemas-do-milnio.html
http://www.cienciahoje.pt/index.php?oid=9551&op=all

sábado, 31 de julho de 2010

Função Quadrática: forma canônica

Qual o gráfico da função f(x)=3(x+4)^2-11

?

Se marcarmos alguns pontos do gráico desta função logo veremos que é uma parábola. Não é de admirar, pois 3(x+4)^2-11=3(x^2+8x+16)-11=3x^2+24x+37

. Ou seja, é uma função polinomial do 2º grau escrita de uma forma diferente.

O interessante en escrever a função desta forma é que assim ficam explicitos algumas propriedades desta função, por exemplo: o valor 3(x+4)^2

é sempre positivo ou zero quando x=-4

, mas

que é o menor valor que esta função pode assumir, ou o valor do vértice. Encontrar os zeros desta função também não é complicado, basta resolver 3(x+4)^2-11=0

, somando 11, dividindo por 3 extraindo a raíz quadrada e subtraindo 4 vemos que isto é o suficiente para encontrarmos $x=-4\pm\sqrt{\frac{11}{3}}$ .

A função f(x)=A(x+B)^2+C

com A, B e C reais é chamada de a forma canônica da função do 2º grau. O maior problema é como colocar , por exemplo a função f(x)=2x^2-4x+8

, na forma canônica? Para responder esta questão vamos fazer por passos.

Primeiramente colocamos o coeficiente de x² (2) em evidência, ficando com:

O maior trunfo nestes procedimentos é somar e subtrair um número para que encontremos um quadrado perfeito dentro do parenteses. Não é complicado encontrar este número, para isso recorremos ao produto notável (x_y)^2=x^2+3yx+y^2

. O número que queremos somar e subtrair dentro do parenteses será denotado por y^2

. Note que ele deve satisfazer 2yx=-2x

, ou seja, devemos ter y=-1

. Assim a função fica:

$\begin{array}{l}f(x)=2(x^2-2x+y^2-y^2+4) \\ f(x)=2(x^2+2(-1)x+(-1)^2-(-1)^2+4)\end{array}$

Repare que, por construção, as três primeiras parcelas dentro do parenteses é igual a um quadrado perfeito. Explicitamente x^2+2(-1)x+(-1)^2=(x-1)^2

. Fazendo esta substituição temos:

$\begin{array}{l} f(x)=2(x^2+2(-1)x+(-1)^2-(-1)^2+4)\\ f(x)=2((x-1)^2+3)\end{array}$

E por fiz, distribuindo 2 dentro do parenteses econtramos a forma canônica da função:

Resta a questão de generalizar isso para a função genérica $f(x)=ax^2+bx+c, a\neq0$ . Para isso procedemos da mesma forma.

1_Coloque o coeficiente de em evidência

$f(x)=a\left(x^2+\frac{b}{a}x+\frac{c}{a}\right)$

2_Some e suntraia um número de tal forma que $2yx=\frac{a}{b}x\Rightarrow y=\frac{b}{2a}\Rightarrow y^2=\frac{b^2}{4a^2}$ .

$f(x)=a\left(x^2+\frac{b}{a}x+\frac{b^2}{4a^2}-\frac{b^2}{4a^2}+\frac{c}{a}\right)$

3_Fatore as três primeiras parcelas que, segundo a soma que fizemos, é um quadrado perfeito.

$f(x)=a\left(\left(x+\frac{b^}{2a}\right)^2-\frac{b^2}{4a^2}+\frac{c}{a}\right)$

4_Some as outras duas parcelas $-\frac{b^2}{4a^2}+\frac{c}{a}\right$ .

$f(x)=a\left(\left(x+\frac{b^}{2a}\right)^2-\frac{b^2-4ac}{4a^2}\right)$ .

5_Distribua a dentro do parenteses.

$f(x)=a\left(x+\frac{b^}{2a}\right)^2-\frac{b^2-4ac}{4a}$

A expressão b^2-4ac

é chamada de discriminante da equação do 2º grau e é representada pela letra grega $\Delta$ (delta maiúscula). Assim, podemos também escrever a função f(x)=ax^2+bx+c

como:

$f(x)=a\left(x+\frac{b^}{2a}\right)^2-\frac{\Delta}{4a}$

domingo, 25 de julho de 2010

LaTeX como um meio de comunicação pela web

Normalmente que discute matemática por sites de interação social como orkut, facebook, twitter, blogger entre outros tem uma certa dificuldade de comunicar certos símbolos e fórmulas.

Uma alternativa que venho apresentar aqui, não para suprimir esta dificuldade mas pelo menos amenizá-la, é um pluging para o firefox que permite a edição de textos matemáticos em linguagem LaTeX. Para isso é preciso de três atributos:

Firefox 1.5 ou superior instalado
Pluging greasemonkey instalado: este pluging permite personalizar a forma como é exibida uma página web usando pequenos pedaços de JavaScript.
O Script http://thewe.net/tex/textheworld6.user.js instalado: Este é o código em JavaScript que permitirá a visualização de formulas pela internet.

Para escrever em linguagem matemática (frações, raízes, potências, funções entre outros símbolos) o conteúdo deve ser escrito em linguagem TeX, iniciado por [; e finalizado por ;]. A sintaxe básica do LaTeX pode ser consultada no site do Wikipedia: aqui

Se você fez a instalação corretamente do plunging verá abaixo um conjunto de símbolos matemáticos:

[;y = x^4 - 3x^2 + 5;]

[;\frac{-b\pm\sqrt{b^2-4ac}}{2a};]

[;e^{i\sqrt{-1}}+1=0;]

[;S=\sum_{k=1}^{10}{f(x_k)};]

[;\begin{cases}3x + 4y =10 \\ 2x - 5y = 25\end{cases};]

[;I\,=\,\int_{-\infty}^{+\infty}e^{-x^2}\, dx;]

[;\color{1} f(x) = \frac{sin^2 \theta} {\sqrt{\beta}};]

[;\lim_{n \to \infty}x_n;]

quinta-feira, 15 de julho de 2010

Soneto de Promessa

Coração vermelho, vibrante inconsciente;
Causando um terremoto, abalando a alma;
Próximo a ela é feliz, sempre contente;
E não se igual em qualquer flora ou fauna.

Viver por ela, minha inspiração;
Quero sempre sentir este amor excitante;
Beijar, tocar e ouvir sua canção.

Estar sempre junto, respeitando com igualdade;
Não vez ou outra, mas sempre constante;
Não ser uma máquina, porem parte da humanidade.

Pode ser, entretanto que o amor não dure;
Que em cada grão da ampulheta se torna diferente;
Se for o caso quer lutar para que o amor madure;
E que a cada instante o viva mais intensamente.

Aline, te amo.

sexta-feira, 4 de junho de 2010

Vértice da Função do 2º grau

Sabemos que o gráfico de uma função do 2º grau é uma parábola no plano $\mathbb R^2$ . Em algumas situações é interessante determinar em que ponto está situado o vértice da parábola, ponto este que é o máximo (se a concavidade da parábola está para cima) ou mínimo (caso contrário) valor que a função atinge.

Para encontrar este vértice consideramos 3 possíveis situações em que se pode encontrar a função: 1 - a função tem duas raízes; 2 - a função tem uma única raiz; 3 - a função não tem raiz. Estas três situações são ilustradas abaixo:

Em todo caso, encontrar as raízes de uma função f(x)=ax^2+bx+c é o mesmo que resolver a equação que como sabemos possui ou não solução real dependendo do discriminante $\Delta=b^2-4ac$ . As condições são:

possui 2 raízes reais se ;
uma raiz real se $\Delta=0$ ;
nenhuma raiz real se $\Delta<0$ .

Observando a figura acima e considerando estas 3 condições de $\Delta$ podemos notar que a função f(x)=ax^2+bx+c terá valor no vértice igual a zero se seu discriminante for igual a zero. Podemos ver isto nos exemplos abaixo:

Agora, se é o valor que uma função f(x)=ax^2+bx+c

assume em seu vértice ( pode ser máximo ou mínimo) consideramos a função .

Podemos notar que a função além de continuar sendo uma função do 2º grau, também o valor que assume no vértice é zero, isto pode ser verificado notando que ao somar a estamos apenas transladando o seu gráfico verticalmente, isto é, se f(x_v)